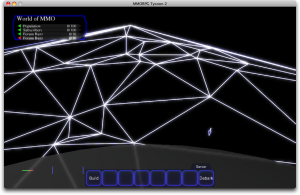
What you’re looking at here is known in mathematic circles as a Delaunay tesselation (viewed from a skewed angle). Basically, pick a bunch of random points in space, then join those points together with lines in such a way as to make the nicest triangles possible. Of course, being a mathematics thing, there’s actually a very precise definition of what “nicest triangles possible” means, but your own intuitive definition probably roughly matches the mathematical one; just try to space the triangles as evenly as possible, while still touching each random point we selected earlier. (The mathematical rule is that for each triangle, if you were to make a circle which touched all three points of that triangle, then no vertex of any other triangle would be inside that circle. But if you’re anything like me, trying to visualise that criteria for very long will probably make your brain hurt)
Incidentally, it’s worth mentioning that in this screenshot, we’re looking at a completely flat surface; none of these points are any higher than the others; if you think you see hills or valleys, that’s just a trick of the perspective.
Anyhow. At this point you’re probably asking yourself, “Why has Trevor spent the last two days implementing this somewhat obscure mathematics algorithm?” Well, you can probably guess from the high-up viewpoint in the screenshot that we’re looking at a full MMORPG map again (with no water), and you may well remember that I wasn’t happy with the boxiness of the old region boundaries. But these triangles would be rotten if used as region boundaries; they’re a terrible shape and many are far too small to fit playable MMORPG regions into. Well, the answer is quite simply that a Delaunay tesselation like the one pictured here can easily be converted into a Voronoi diagram. And a Voronoi diagram just happens to be precisely what I need for nice, interestingly-shaped regions. But it’s late; I’m not going to finish the Delaunay->Voronoi conversion today, so I’m just posting a screen capture of the Delaunay tesselation, instead.
Tomorrow, a Voronoi diagram and a proper explanation about what they are, and why they’re awesome.
